6.4 定制用户自己的邻居采样器¶
虽然DGL提供了一些邻居采样器,但有时用户还是希望编写自己的采样器。 本节会说明如何编写用户自己的采样器并将其加入到GNN的训练框架中。
回想一下在 How Powerful are Graph Neural Networks 的论文中,消息传递的定义是:
其中, \(\rho^{(l)}\) 和 \(\phi^{(l)}\) 分别是可自定义的消息函数与聚合函数, \(\mathcal{N}(v)\) 为有向图 \(\mathcal{G}\) 上的节点 \(v\) 的前驱节点(或无向图中的邻居)。
以下图为例,假设红色节点为需要更新的目标节点:
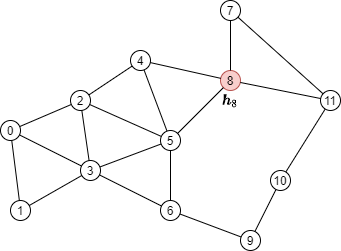
消息传递需要聚集其邻居(绿色节点)的节点特征,如下图所示:
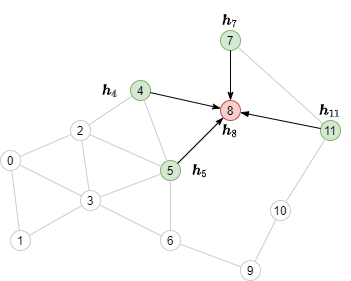
理解邻居采样的工作原理¶
在介绍DGL中邻居采样的用法之前,这里先解释一下邻居采样的工作原理。下文继续使用上述的例子。 首先定义一个如上图所示的DGLGraph。
import torch
import dgl
src = torch.LongTensor(
[0, 0, 0, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 10,
1, 2, 3, 3, 3, 4, 5, 5, 6, 5, 8, 6, 8, 9, 8, 11, 11, 10, 11])
dst = torch.LongTensor(
[1, 2, 3, 3, 3, 4, 5, 5, 6, 5, 8, 6, 8, 9, 8, 11, 11, 10, 11,
0, 0, 0, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 10])
g = dgl.graph((src, dst))
该例子的目标是计算单个节点(节点8)的输出。DGL将需要计算GNN输出的节点称为 种子节点 。
找出消息传递的依赖¶
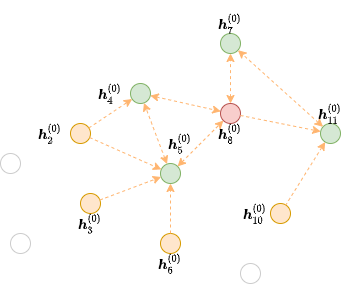
假设要使用2层GNN计算种子节点8(红色点)的输出:
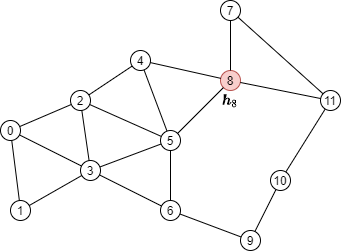
其消息传递的计算公式如下:
从公式中可以看出,要计算 \(\boldsymbol{h}_8^{(2)}\),需要下图中的来自节点4、5、7和11(绿色点)的消息。
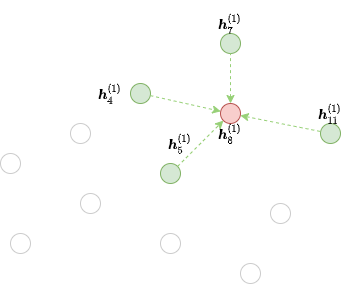
上图中隐去了和计算不相关的边,仅仅保留了输出节点所需要收集消息的边。DGL称它们为红色节点8在第二个GNN层的 边界子图。
DGL实现了多个可用于生成边界的函数。例如,
dgl.in_subgraph() 是一个生成子图的函数,该子图包括初始图中的所有节点和指定节点的入边。
用户可以将其用作沿所有入边传递消息的边界。
frontier = dgl.in_subgraph(g, [8])
print(frontier.all_edges())
想了解更多的相关函数,用户可以参考 Subgraph Extraction Ops 和 dgl.sampling。
在DGL中,任何具有与初始图相同的节点的图都可以用作边界。这点在之后的 实现一个自定义邻居采样器 章节中也会提到。
多层小批量消息传递的二分计算图¶
从上图中可以看到,从 \(\boldsymbol{h}_\cdot^{(1)}\) 计算 \(\boldsymbol{h}_8^{(2)}\) 只需要节点4, 5, 7, 8和11(绿色和红色节点)作为输入。 原图上的其他节点是不参与计算的,因此直接在边界子图上执行消息传递有很大开销。 因此,DGL对边界子图做了一个转换,把它的计算依赖关系变成了一个小的二分图。 DGL称这种仅包含必要的输入节点和输出节点的二分图为一个 块 (block)。 下图显示了以节点8为种子节点时第二个GNN层所需的块。
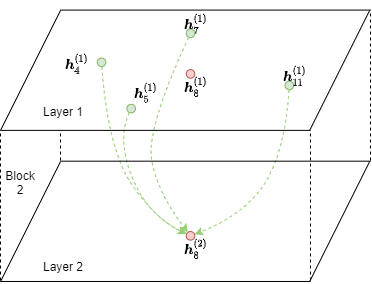
请注意,输出节点也出现在输入节点中。原因是消息传递后的特征组合需要前一层的输出节点表示 (即 \(\phi^{(2)}\))。
DGL提供了 dgl.to_block() 以将任何边界转换为块。其中第一个参数指定边界,
第二个参数指定输出节点。例如,可以使用以下代码将上述边界转换为输出节点为8的块。
output_nodes = torch.LongTensor([8])
block = dgl.to_block(frontier, output_nodes)
要查找给定节点类型的输入节点和输出节点的数量,可以使用
dgl.DGLGraph.number_of_src_nodes() 和
dgl.DGLGraph.number_of_dst_nodes() 方法。
num_input_nodes, num_output_nodes = block.number_of_src_nodes(), block.number_of_dst_nodes()
print(num_input_nodes, num_output_nodes)
可以通过 dgl.DGLGraph.srcdata 和
dgl.DGLGraph.srcnodes 访问该块的输入节点特征,
并且可以通过 dgl.DGLGraph.dstdata 和
dgl.DGLGraph.dstnodes 访问其输出节点特征。
srcdata/dstdata 和 srcnodes/dstnodes
的语法与常规图中的 dgl.DGLGraph.ndata 和 dgl.DGLGraph.nodes 相同。
block.srcdata['h'] = torch.randn(num_input_nodes, 5)
block.dstdata['h'] = torch.randn(num_output_nodes, 5)
如果是从图中得到的边界,再由边界转换成块,则可以通过以下方式直接读取块的输入和输出节点的特征。
print(block.srcdata['x'])
print(block.dstdata['y'])
用户可以通过 dgl.NID 得到块中输入节点和输出节点的初始节点ID,可以通过 dgl.EID
得到边ID到输入边界中边的初始ID的映射。
输出节点
DGL确保块的输出节点将始终出现在输入节点中。如下代码所演示的,在输入节点中,输出节点的ID位于其它节点之前。
input_nodes = block.srcdata[dgl.NID]
output_nodes = block.dstdata[dgl.NID]
assert torch.equal(input_nodes[:len(output_nodes)], output_nodes)
因此,在用多层图神经网络时,中间某一层对应的边界需要包含该层及所有后续层计算涉及边的目标节点。例如,考虑以下边界
其中红色和绿色节点(即节点4、5、7、8和11)都是后续图神经网络层计算中某条边的目标节点。 以下代码由于输出节点未覆盖所有这些节点,将会报错。
dgl.to_block(frontier2, torch.LongTensor([4, 5])) # ERROR
但是,输出节点可以比以上节点包含更多节点。下例的输出节点包含了没有入边的孤立节点。 输入节点和输出节点将同时包含这些孤立节点。
# 节点3是一个孤立节点,没有任何指向它的边.
block3 = dgl.to_block(frontier2, torch.LongTensor([4, 5, 7, 8, 11, 3]))
print(block3.srcdata[dgl.NID])
print(block3.dstdata[dgl.NID])
异构图上的采样¶
块也可用于异构图。假设有如下的边界:
hetero_frontier = dgl.heterograph({
('user', 'follow', 'user'): ([1, 3, 7], [3, 6, 8]),
('user', 'play', 'game'): ([5, 5, 4], [6, 6, 2]),
('game', 'played-by', 'user'): ([2], [6])
}, num_nodes_dict={'user': 10, 'game': 10})
可以创建一个如下的块,块的输出节点为 User 节点3、6、8和 Game 节点2、6。
hetero_block = dgl.to_block(hetero_frontier, {'user': [3, 6, 8], 'block': [2, 6]})
对于这个块,用户可以按节点类型来获取输入节点和输出节点:
# 输入的User和Game节点
print(hetero_block.srcnodes['user'].data[dgl.NID], hetero_block.srcnodes['game'].data[dgl.NID])
# 输出的User和Game节点
print(hetero_block.dstnodes['user'].data[dgl.NID], hetero_block.dstnodes['game'].data[dgl.NID])
实现一个自定义邻居采样器¶
前面章节里给出了以下用在节点分类任务的邻居采样器。
sampler = dgl.dataloading.MultiLayerFullNeighborSampler(2)
想实现自定义的邻居采样策略,用户可以将采样器对象替换为自定义的采样器对象。
为此,先来看一下
MultiLayerFullNeighborSampler
的父类
BlockSampler。
BlockSampler
负责使用
sample_blocks()
方法从最后一层开始生成一个块的列表。 sample_blocks 的默认实现是向后迭代,生成边界,并将其转换为块。
因此,对于邻居采样,用户仅需要实现sample_frontier()方法。
给定GNN层、初始图和要计算表示的节点,该方法负责为它们生成边界。
同时,用户还必须将GNN的层数传递给父类。
例如, MultiLayerFullNeighborSampler 的实现如下。
class MultiLayerFullNeighborSampler(dgl.dataloading.BlockSampler):
def __init__(self, n_layers):
super().__init__(n_layers)
def sample_frontier(self, block_id, g, seed_nodes):
frontier = dgl.in_subgraph(g, seed_nodes)
return frontier
dgl.dataloading.neighbor.MultiLayerNeighborSampler
是一个更复杂的邻居采样器类,它允许用户为每个节点采样部分邻居节点以汇聚信息,如下所示。
class MultiLayerNeighborSampler(dgl.dataloading.BlockSampler):
def __init__(self, fanouts):
super().__init__(len(fanouts))
self.fanouts = fanouts
def sample_frontier(self, block_id, g, seed_nodes):
fanout = self.fanouts[block_id]
if fanout is None:
frontier = dgl.in_subgraph(g, seed_nodes)
else:
frontier = dgl.sampling.sample_neighbors(g, seed_nodes, fanout)
return frontier
虽然上面的函数可以生成边界,但是任何拥有与初始图相同节点的图都可用作边界。
例如,如果要以某种概率将种子节点的入边随机剔除,则可以按照以下方式简单地定义采样器:
class MultiLayerDropoutSampler(dgl.dataloading.BlockSampler):
def __init__(self, p, num_layers):
super().__init__(num_layers)
self.p = p
def sample_frontier(self, block_id, g, seed_nodes, *args, **kwargs):
# 获取种 `seed_nodes` 的所有入边
src, dst = dgl.in_subgraph(g, seed_nodes).all_edges()
# 以概率p随机选择边
mask = torch.zeros_like(src).bernoulli_(self.p)
src = src[mask]
dst = dst[mask]
# 返回一个与初始图有相同节点的边界
frontier = dgl.graph((src, dst), num_nodes=g.number_of_nodes())
return frontier
def __len__(self):
return self.num_layers
在实现自定义采样器后,用户可以创建一个数据加载器。这个数据加载器使用用户自定义的采样器, 并且遍历种子节点生成一系列的块。
sampler = MultiLayerDropoutSampler(0.5, 2)
dataloader = dgl.dataloading.NodeDataLoader(
g, train_nids, sampler,
batch_size=1024,
shuffle=True,
drop_last=False,
num_workers=4)
model = StochasticTwoLayerRGCN(in_features, hidden_features, out_features)
model = model.cuda()
opt = torch.optim.Adam(model.parameters())
for input_nodes, blocks in dataloader:
blocks = [b.to(torch.device('cuda')) for b in blocks]
input_features = blocks[0].srcdata # 返回一个字典
output_labels = blocks[-1].dstdata # 返回一个字典
output_predictions = model(blocks, input_features)
loss = compute_loss(output_labels, output_predictions)
opt.zero_grad()
loss.backward()
opt.step()
异构图上自定义采样器¶
为异构图生成边界与为同构图生成边界没有什么不同。只要使返回的图具有与初始图相同的节点,
就可以正常工作。例如,可以重写上面的 MultiLayerDropoutSampler 以遍历所有的边类型,
以便它也可以在异构图上使用。
class MultiLayerDropoutSampler(dgl.dataloading.BlockSampler):
def __init__(self, p, num_layers):
super().__init__(num_layers)
self.p = p
def sample_frontier(self, block_id, g, seed_nodes, *args, **kwargs):
# 获取 `seed_nodes` 的所有入边
sg = dgl.in_subgraph(g, seed_nodes)
new_edges_masks = {}
# 遍历所有边的类型
for etype in sg.canonical_etypes:
edge_mask = torch.zeros(sg.number_of_edges(etype))
edge_mask.bernoulli_(self.p)
new_edges_masks[etype] = edge_mask.bool()
# 返回一个与初始图有相同节点的图作为边界
frontier = dgl.edge_subgraph(new_edges_masks, relabel_nodes=False)
return frontier
def __len__(self):
return self.num_layers